Attention in Neural Networks - 4. Sequence-to-Sequence (Seq2Seq) (3)
25 Jan 2020 | Attention mechanism Deep learning PytorchAttention Mechanism in Neural Networks - 4. Sequence-to-Sequence (Seq2Seq) (3)
In the previous posting, we saw how to prepare machine translation data for Seq2Seq. In this posting, let’s implement the Seq2Seq model delineated by Cho et al. (2014) with Pytorch with the prepared data.
Data Preparation
After data processing, we have four variables that contain critical information for learning a Seq2Seq model. In the previous posting, we named them eng_words, deu_words, eng_sentences, deu_sentences. eng_words and deu_words contain unique words in source (English) and target (German) sentences. In my processed data, there were 9,199 English and 16,622 German words but note that it can differ in your results since we randomly sampled 50,000 sentences.
eng_words, deu_words = list(eng_words), list(deu_words)
# print the size of the vocabulary
print(len(eng_words), len(deu_words))
9199 16622
eng_sentences and deu_sentences contain source (English) and target(German) sentences in which words are indexed according to the position in eng_words and deu_words lists. For instance, first elements in our lists were [4977, 8052, 5797, 8153, 5204, 2964, 6781, 7426] and [9231, 8867, 7020, 936, 13206, 5959, 13526]. And they correspond to English and German sentences ['<sos>', 'so', 'far', 'everything', 'is', 'all', 'right', '<eos>'] and ['<sos>', 'soweit', 'ist', 'alles', 'in', 'ordnung', '<eos>'].
print(eng_sentences[0])
print([eng_words[x] for x in eng_sentences[0]])
print(deu_sentences[0])
print([deu_words[x] for x in deu_sentences[0]])
[4977, 8052, 5797, 8153, 5204, 2964, 6781, 7426]
['<sos>', 'so', 'far', 'everything', 'is', 'all', 'right', '<eos>']
[9231, 8867, 7020, 936, 13206, 5959, 13526]
['<sos>', 'soweit', 'ist', 'alles', 'in', 'ordnung', '<eos>']
Parameter setting
Now, let’s move onto setting hyperparameters for our Seq2Seq model. Key parameters and their descriptions are as below.
MAX_SENT_LEN: maximum sentence length of the source (English) sentenceENG_VOCAB_SIZE,DEU_VOCAB_SIZE: number of unique tokens (words) in English and German, respectivelyNUM_EPOCHS: number of epochs to train the Seq2Seq modelHIDDEN_SIZE: dimensionality of the hidden space in LSTM (or any RNN variant of choice)EMBEDDING_DIM: dimensionality of the word embedding space
We set the parameters as below. Note that NUM_EPOCHS, HIDDEN_SIZE, and EMBEDDING_DIM variables can be arbitrarily set by the user as in any other neural network architecture. You are strongly encouraged to test other parameter settings and compare the results.
MAX_SENT_LEN = len(max(eng_sentences, key = len))
ENG_VOCAB_SIZE = len(eng_words)
DEU_VOCAB_SIZE = len(deu_words)
NUM_EPOCHS = 1
HIDDEN_SIZE = 128
EMBEDDING_DIM = 30
DEVICE = torch.device('cuda')
RNN in Pytorch
Prior to implemeting the encoder and decoder, let’s briefly review the inner workings of RNNr and how they are implemented in Pytorch. We will implement the Long Short-Term Memory (LSTM), which is a popular variant of RNN.
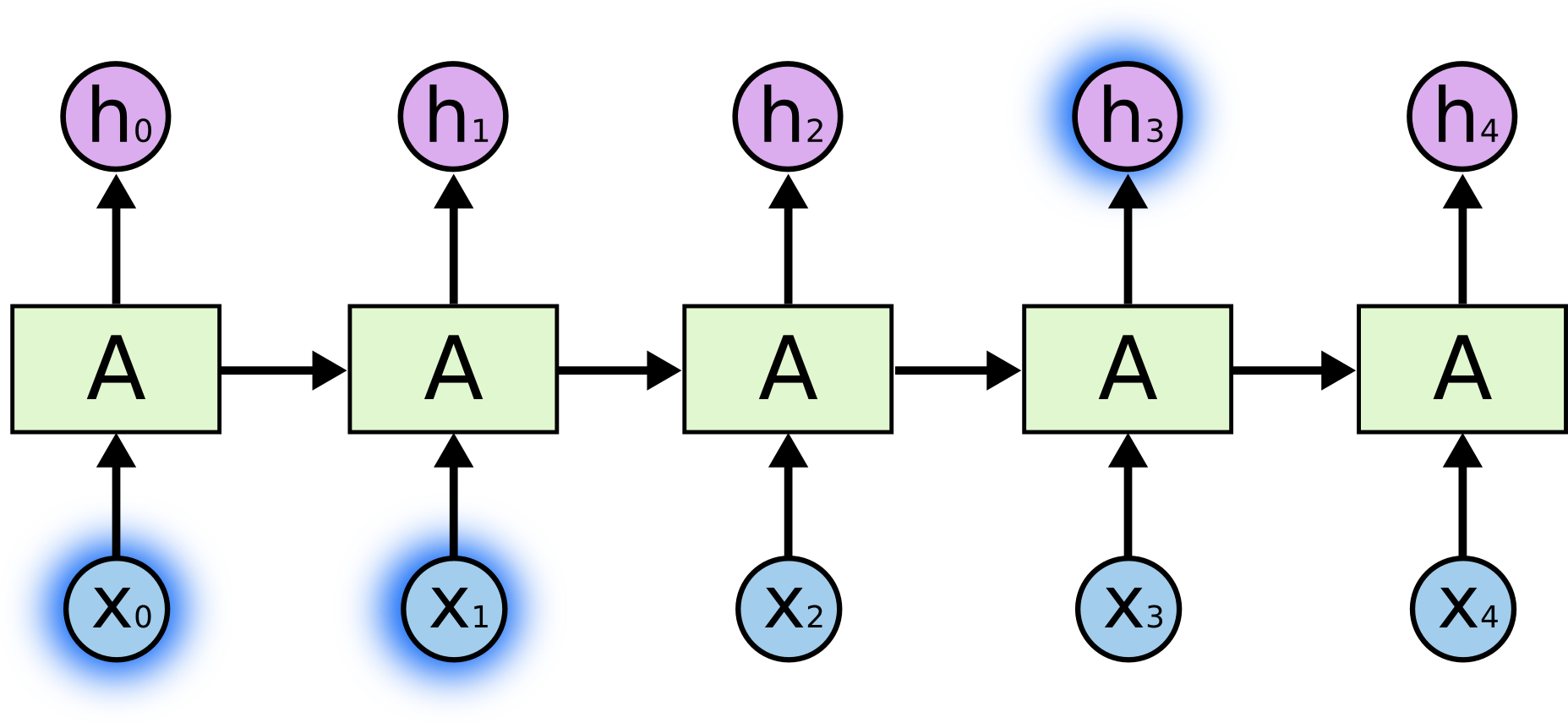
RNNs in general are used for modeling temporal dependencies among inputs in consecutive timesteps. Unlike feed-forward neural networks, they have “loops” in the network, letting the information flow between timesteps. Such information is stored and passed onto as “hidden states.” For each input (\(x_i\)), there is a corresponding hidden state (\(h_i\)) that preserves information at that time step \(i\). And that hidden state is also an input at the next time step with \(x_{i+1}\). At the first timestemp (0), they are randomly initialized.
In addition to the hidden state, there is additional information that is passed onto the next state, namely the cell state (\(c_i\)). The math behind it is complicated but I won’t be going into detail . For the sake of simplicity, we can regard it as another type of hidden state in this posting. For more information, please refer to Hochreiter et al. (1997).
Once we understand the inner workings of RNN, it is fairly straightforward to implement it with Pytorch.
import torch.nn as nn
lstm = nn.LSTM(input_size = 10,
hidden_size = 5,
num_layers = 1)
- Create LSTM layer: there are a few parameters to be determined. Some of the essential ones are
input_size,hidden_size, andnum_layers.input_sizecan be regarded as a number of features. Each input in each timestemp is an n-dimensional vector with n =input_size.hidden_sizeis the dimensionality of the hidden state. Each hidden state is an m-dimensional vector with m =hidden_size. Finallynum_layersdetermines the number of layers in the LSTM layer. Setting it over 3 makes it a deep LSTM.
## inputs to LSTM
# input data (seq_len, batch_size, input_size)
x0 = torch.from_numpy(np.random.randn(1, 64, 10)).float()
- Determine input size: The shape of inputs to the LSTM layer is
(seq_len, batch_size, input_size).seq_lendetermines the length of the sequence, or the number of timesteps. In the machine translation task, this should be the number of source (or target) words in the instance.input_sizeshould be the same as one defined when creating the LSTM layer.
h0, c0 = torch.from_numpy(np.zeros((1, 64, 5))).float(), torch.from_numpy(np.zeros((1, 64, 5))).float()
- Initialize hidden & cell states: hidden and cell states have the same shape
(num_layers, batch_size, hidden_size)in general. Note that we need not considerseq_lensince hidden and cell states are refreshed at each time step.
xn, (hn, cn) = lstm(x0, (h0, c0))
print(xn.shape) # (seq_len, batch_size, hidden_size)
print(hn.shape, cn.shape) # (num_layers, batch_size, hidden_size)
torch.Size([1, 64, 5])
torch.Size([1, 64, 5]) torch.Size([1, 64, 5])
- Pass the input and hidden/cell states to LSTM: Now we just need to pass the input and states to the LSTM layer. Note that the hidden and cell states are provided in a single tuple (
h0, c0). The output sizes are identical to the inputs.
If you want to learn more about RNNs in Pytorch, please refer to Pytorch Tutorial on RNN.
Encoder
Now, we have to construct the neural network architecture for Seq2Seq. Here, we construct the encoder and decoder network separately since it can be better understood that way.
Encoder is a relatively simple neural network consisting of embedding and RNN layers. We inject each word in the source sentence (English words in this case) to LSTM after embedding. Note that we have to set three parameters for the encoder network - vocab_size, hidden_size, and embedding_dim. They will correspond to ENG_VOCAB_SIZE, HIDDEN_SIZE, and EMBEDDING_DIM variables defined above.
class Encoder(nn.Module):
def __init__(self, vocab_size, hidden_size, embedding_dim):
super(Encoder, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_size)
def forward(self, x, h0, c0):
x = self.embedding(x).view(1, 1, -1)
out, (h0, c0) = self.lstm(x, (h0, c0))
return out, (h0, c0)
The “hidden state” (h0) from the final source word will be memorized and passed onto the decoder as an input. This is a fixed-sized vector “summary c of the whole input sequence.”
Decoder
Finally, we will have to define the decoder network. The decoder is very similar to the encoder with a slight difference. Other information except the hidden state is discarded in the encoder network. In other words, all information from the input sentence is summarized in the hidden state. Nevertheless, in the decoder, a previous (predicted) word should be passed onto the next LSTM cell for the next prediction. Therefore, we generate another dense layer followed by a softmax activation function to track the predicted word and pass them onto the next step.
class Decoder(nn.Module):
def __init__(self, vocab_size, hidden_size, embedding_dim):
super(Decoder, self).__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_size)
self.dense = nn.Linear(hidden_size, vocab_size)
self.softmax = nn.LogSoftmax(dim = 1)
def forward(self, x, h0, c0):
x = self.embedding(x).view(1, 1, -1)
x, (h0, c0) = self.lstm(x, (h0, c0))
x = self.softmax(self.dense(x.squeeze(0)))
return x, (h0, c0)
As we defined classes to generate the encoder and decoder, we now just have to create and train them!
References
- Cho et al. (2014)
- Hochreiter et al. (1997)
- NLP FROM SCRATCH: TRANSLATION WITH A SEQUENCE TO SEQUENCE NETWORK AND ATTENTION
- Understanding LSTM Networks
In this posting, we implemented the Seq2Seq model with Pytorch. In the next posting, let’s look into how we can train and evaluate them with the prepared data. Thank you for reading.