케라스와 함께하는 쉬운 딥러닝 (4) - 뉴럴 네트워크의 학습 과정 개선하기
22 Apr 2018 | Python Keras Deep Learning 케라스다층 퍼셉트론 4 (Improving techniques for training neural networks)
Objective: 인공신경망 모델을 효율적으로 학습시키기 위한 개선 방법들에 대해 학습한다.
- 가중치 초기화(Weight Initialization)
- 활성함수(Activation Function)
- 최적화(Optimization)
MNIST 데이터 셋 불러오기
# 케라스에 내장된 mnist 데이터 셋을 함수로 불러와 바로 활용 가능하다
from keras.datasets import mnist
import matplotlib.pyplot as plt
(X_train, y_train), (X_test, y_test) = mnist.load_data()
plt.imshow(X_train[0]) # show first number in the dataset
plt.show()
print('Label: ', y_train[0])

plt.imshow(X_test[0]) # show first number in the dataset
plt.show()
print('Label: ', y_test[0])

데이터 셋 전처리
앞서 언급했다시피, MNIST 데이터는 흑백 이미지 형태로, 2차원 행렬(28 X 28)과 같은 형태라고 할 수 있다.

하지만 이와 같은 이미지 형태는 우리가 지금 활용하고자 하는 다층 퍼셉트론 모델에는 적합하지 않다. 다층 퍼셉트론은 죽 늘어놓은 1차원 벡터와 같은 형태의 데이터만 받아들일 수 있기 때문이다. 그러므로 우리는 28 X 28의 행렬 형태의 데이터를 재배열(reshape)해 784 차원의 벡터로 바꾼다.
from keras.utils.np_utils import to_categorical
from sklearn.model_selection import train_test_split
# reshaping X data: (n, 28, 28) => (n, 784)
X_train = X_train.reshape((X_train.shape[0], -1))
X_test = X_test.reshape((X_test.shape[0], -1))
# 학습 과정을 단축시키기 위해 학습 데이터의 1/3만 활용한다
X_train, _ , y_train, _ = train_test_split(X_train, y_train, test_size = 0.67, random_state = 7)
# 타겟 변수를 one-hot encoding 한다
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
(19800, 784) (10000, 784) (19800, 10) (10000, 10)
기본 MLP 모델 학습 및 평가
지난 세션에서 보았듯이, 아무런 개선을 거치지 않은 기본 MLP 모델에 MNIST 데이터를 학습하였을 때에는 21%라는 그리 훌륭하지 않은 결과가 나왔다.
모델 학습 결과 시각화
학습이 진행됨에 따라 달라지는 학습 정확도와 검증 정확도의 추이를 시각화해 본다. 60 에포크가 지난 후에 정확도가 올라가기 시작한다.
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.legend(['training', 'validation'], loc = 'upper left')
plt.show()
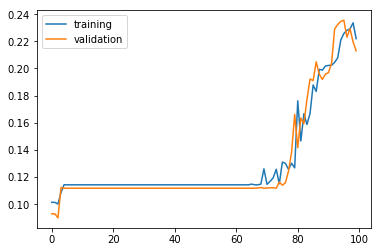
모델 평가
results = model.evaluate(X_test, y_test)
print('Test accuracy: ', results[1])
학습 정확도 21.44%로 랜덤하게 찍는 경우의 예상 정확도(10%)보다는 높게 나왔지만, 그리 만족스러운 수치는 아니다.
Test accuracy: 0.2144
이제 어떻게 우리의 인공 신경망 모델의 MNIST 데이터에 대한 학습을 개선시킬 수 있는지 알아보자!
가중치 초기화(weight initialization)
가중치 초기화 방법을 따로 설정해 주지 않으면 기본적으로 케라스 레이어의 가중치 초기화 방식은 일정 구간 내에서 랜덤하게 찍는 random_uniform이다. 하지만 이러한 방식은 오차 역전파(back propagation) 과정에서 미분한 gradient가 지나치게 커지거나(exploding gradient) 소실되는(vanishing gradient) 문제에 빠질 위험성이 크다(자세한 내용은 여기 참고).
따라서, 어떻게 가중치를 초기화할 것인가에 대한 지속적인 연구가 진행되어 왔고, 이전에 비해 개선된 초기화 방식이 제안되었으며 널리 활용되고 있다. 케라스에서 제공하는 초기화 방식 중 흔히 사용되는 것들은 다음과 같다.
- LeCun 초기화(
lecun_uniform,lecun_normal): 98년도에 얀 르쿤이 제기한 방법으로 최근에는 Xavier나 He 초기화 방식에 비해 덜 사용되는 편이다. - Xavier 초기화(
glorot_uniform,glorot_normal): 케라스에서는glorot이라는 이름으로 되어있는데, 일반적으로는 Xavier Initialization이라고 알려져 있다. 사실 초기화 방식이 제안된 논문의 1저자 이름이 Xavier Glorot이다(출처). 2저자는 유명한 Yoshua Bengio. - He 초기화(
he_uniform,he_normal): ResNet으로도 유명한 마이크로소프트(현재는 Facebook)의 Kaiming He가 2015년에 제안한 가장 최신의 초기화 방식이다. 수식을 보면 Xavier Initialization을 조금 개선한 것인데, 경험적으로 더 좋은 결과를 내었다고 한다.
모델 생성 및 학습
# 이제부터는 함수를 만들어 모델을 생성한다. 이렇게 하면 모듈화와 캡슐화가 되어 관리하기가 훨씬 쉽다.
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, ), kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(50, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(50, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(50, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('sigmoid'))
model.add(Dense(10, kernel_initializer='he_normal')) # use he_normal initializer
model.add(Activation('softmax'))
sgd = optimizers.SGD(lr = 0.001)
model.compile(optimizer = sgd, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 0)
모델 학습 결과 시각화
기존 모델과 비슷하게 60 에포크 이후로 정확도가 올라가기 시작하지만, 한번 탄력을 받자 훨씬 빠르게 올라간다.
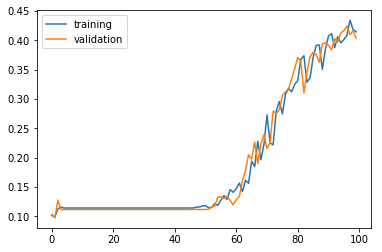
모델 평가
역시 최종 test accuracy도 41%로 기본 모델에 비해 2배 정도 되는 수치를 보인다.
results = model.evaluate(X_test, y_test)
print('Test accuracy: ', results[1])
Test accuracy: 0.4105
활성함수(Activation Function)
기본 모델에서는 활성함수로 시그모이드 함수(sigmoid function)를 활용하였다. 하지만 시그모이드 함수의 경우 입력값이 조금만 커지거나 작아져도 곡선이 평평해져 기울기가 0에 가까워 지는것을 볼 수 있다. 이렇게 되면 랜덤 초기화 방식과 비슷하게 gradient가 소실되는 문제가 발생한다(용어때문에 헷갈리면 기울기 = 미분값 = gradient라고 생각하면 편하다).
조금 다르지만 비슷하게 생긴 탄젠트 하이퍼볼릭(tanh) 함수도 비슷한 문제를 겪으며, 이를 해결하기 위해 나온 함수가 2013년 AlexNet과 함께 혜성처럼 등장한 ReLU (Rectified Linear Unit) 함수이다. 입력값이 0보다 크면 그대로, 0보다 작으면 0으로 출력을 내보내는 어찌보면 무식한(?) 형태이지만 gradient 소실 문제가 발생할 확률을 대폭 줄여주기 때문에 현재 가장 널리 활용되고 있는 활성함수이다. ReLU를 조금 변형한 PReLU, Leaky ReLU, SeLU 등도 제안되었지만, ReLU만큼 자주 사용되지는 않는다.
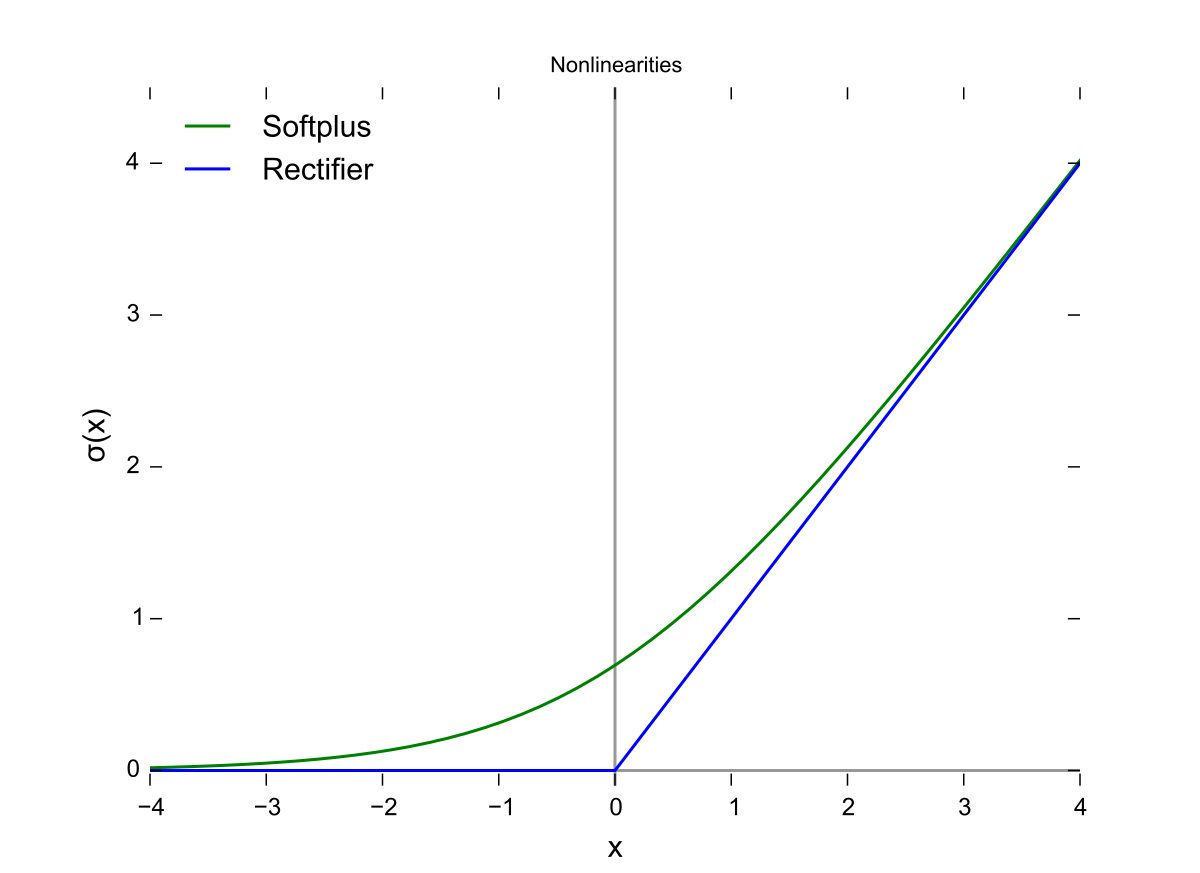
모델 생성 및 학습
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, )))
model.add(Activation('relu')) # use relu
model.add(Dense(50))
model.add(Activation('relu')) # use relu
model.add(Dense(50))
model.add(Activation('relu')) # use relu
model.add(Dense(50))
model.add(Activation('relu')) # use relu
model.add(Dense(10))
model.add(Activation('softmax'))
sgd = optimizers.SGD(lr = 0.001)
model.compile(optimizer = sgd, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 0)
모델 학습 결과 시각화
학습이 이전에 비해 굉장히 빨리되는 것을 볼 수 있다. 학습이 10바퀴 돌기도 전에 학습 오차가 10% 이내로 줄어들며 60 에포크쯤 가서는 학습 오차는 0에 가까워진다.
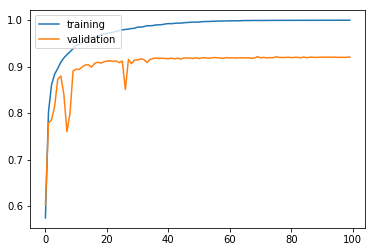
모델 평가
역시 최종 test accuracy도 92%로 이전 모델에 비해 비약적으로 높아진 것을 알 수 있다.
results = model.evaluate(X_test, y_test)
print('Test accuracy: ', results[1])
Test accuracy: 0.9208
최적화(Optimization)
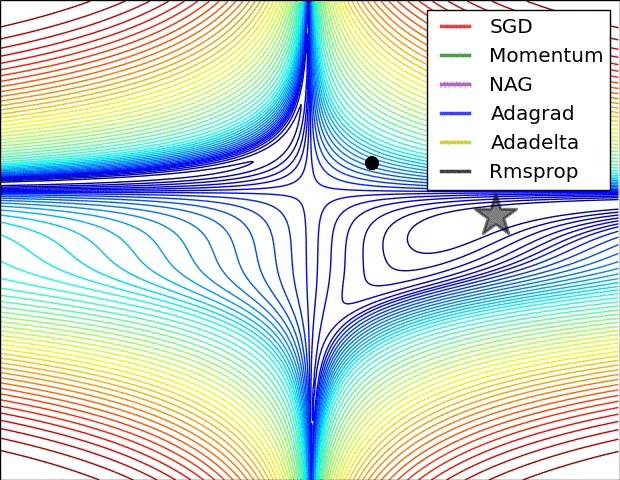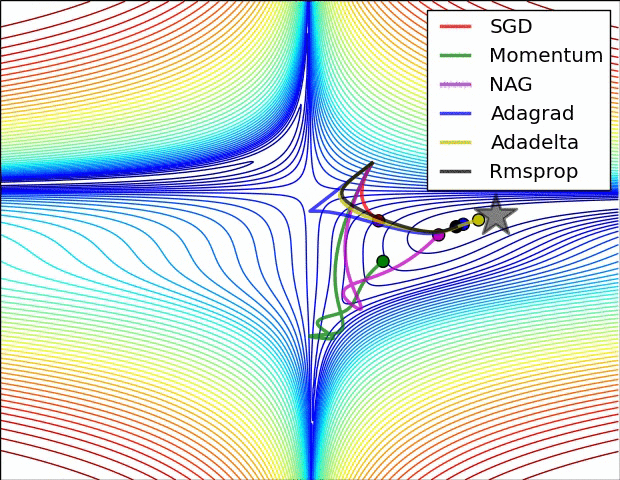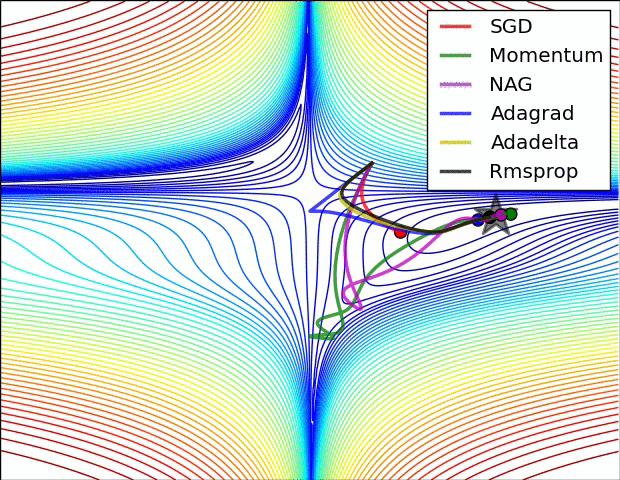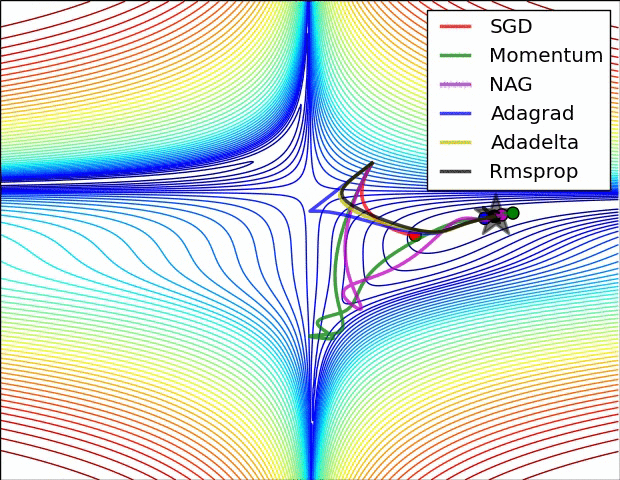
오차 역전파를 활용하는 뉴럴 네트워크의 최적화 방식으로 대부분 경사하강법(SGD; Stochastic Gradient Descent)를 활용한다. 그렇지만 SGD에도 수많은 변용이 존재하며, 각각 장점과 단점을 가지고 있다. 경사하강법을 구현할 때 처음에 스텝의 크기인 learning rate를 설정해 주는데, learning rate를 상황에 따라 계속 변경하면서 학습을 진행하는 adaptive learning methods가 흔히 활용된다(그때그때 실정에 맞추어 스텝의 크기를 바꾸어주다보니 학습이 훨씬 빠르다).
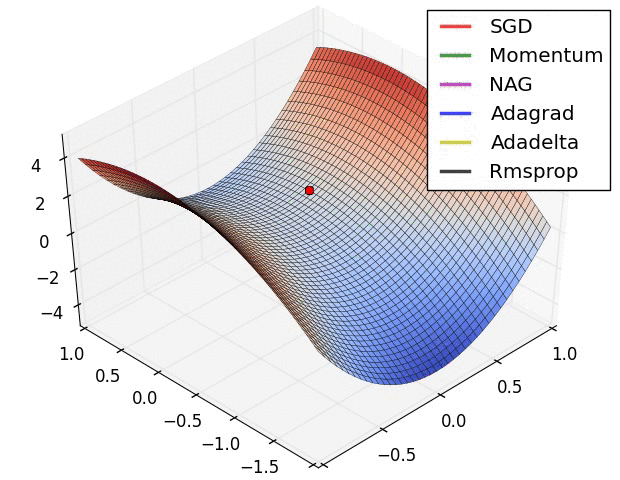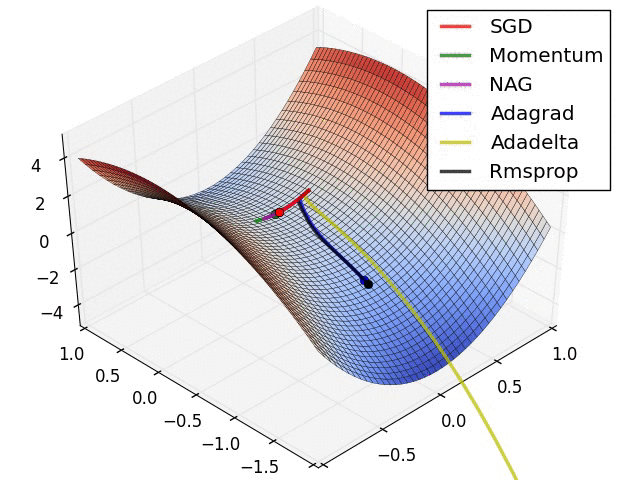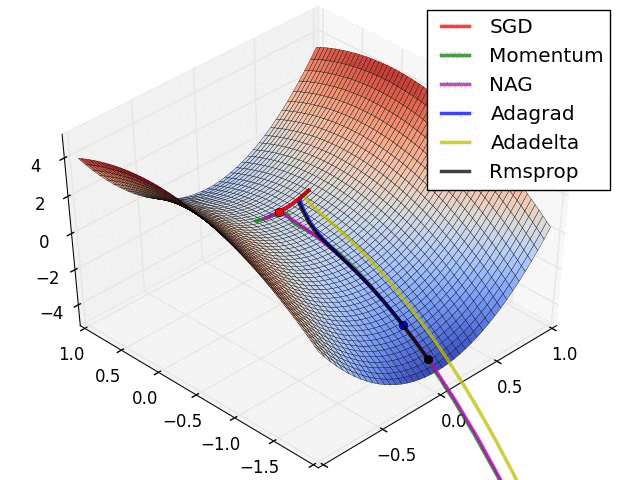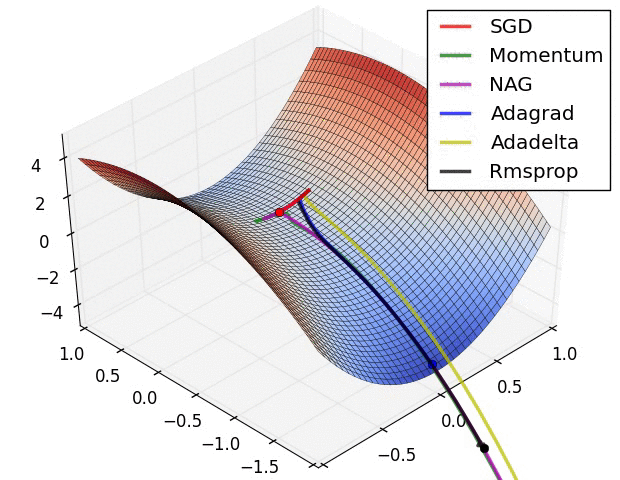
최근에는 RMSprop이나 Adam (RMSprop에 모멘텀의 개념을 접합한 optimizer)을 흔히 사용하며 케라스에서는 둘 다 지원된다.
모델 생성 및 학습
Adam을 써서 최적화를 해보자.
def mlp_model():
model = Sequential()
model.add(Dense(50, input_shape = (784, )))
model.add(Activation('sigmoid'))
model.add(Dense(50))
model.add(Activation('sigmoid'))
model.add(Dense(50))
model.add(Activation('sigmoid'))
model.add(Dense(50))
model.add(Activation('sigmoid'))
model.add(Dense(10))
model.add(Activation('softmax'))
adam = optimizers.Adam(lr = 0.001) # use Adam optimizer
model.compile(optimizer = adam, loss = 'categorical_crossentropy', metrics = ['accuracy'])
return model
model = mlp_model()
history = model.fit(X_train, y_train, validation_split = 0.3, epochs = 100, verbose = 0)
모델 학습 결과 시각화
이번에도 학습이 이전에 비해 굉장히 빨리될 뿐 아니라, 학습/검증 정확도의 증가가 안정적으로 이루어지는 것을 볼 수 있다. 50에포크쯤 가서 90% 이상의 정확도에 안착하는 것을 볼 수 있다.
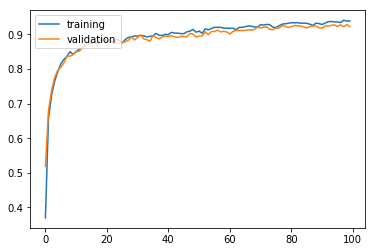
모델 평가
역시 최종 test accuracy도 92%로 이전 모델에 비해 비약적으로 높아진 것을 알 수 있다.
results = model.evaluate(X_test, y_test)
print('Test accuracy: ', results[1])
Test accuracy: 0.9248
이번 포스팅에서는 뉴럴 네트워크의 학습 과정을 개선시킬 수 있는 세 가지 방식에 대해 알아봤으며, 이를 적용해본 결과 92%라는 이전에 비해 훨씬 높은 검증 정확도를 얻을 수 있었다. 이처럼 케라스에서 코드를 몇 줄 바꾸는 간단한 과정으로 비약적인 정도의 개선과 변화를 가지고 올 수 있다는 것이 케라스의 가장 큰 장점이 아닌가 싶다.
다음 포스팅에서는 학습 과정을 개선시키는 3가지 방식에 대해서 더 알아보자.
전체 코드
본 실습의 전체 코드는 여기에서 열람하실 수 있습니다!
