Attention Mechanism in Neural Networks - 13. Various attention mechanisms (2)

In the previous posting, we saw various attention methods explained by Luong et al. (2015). In this posting, let’s try implemeting differnt scoring functions with Pytorch.

Simplified concat (additive)

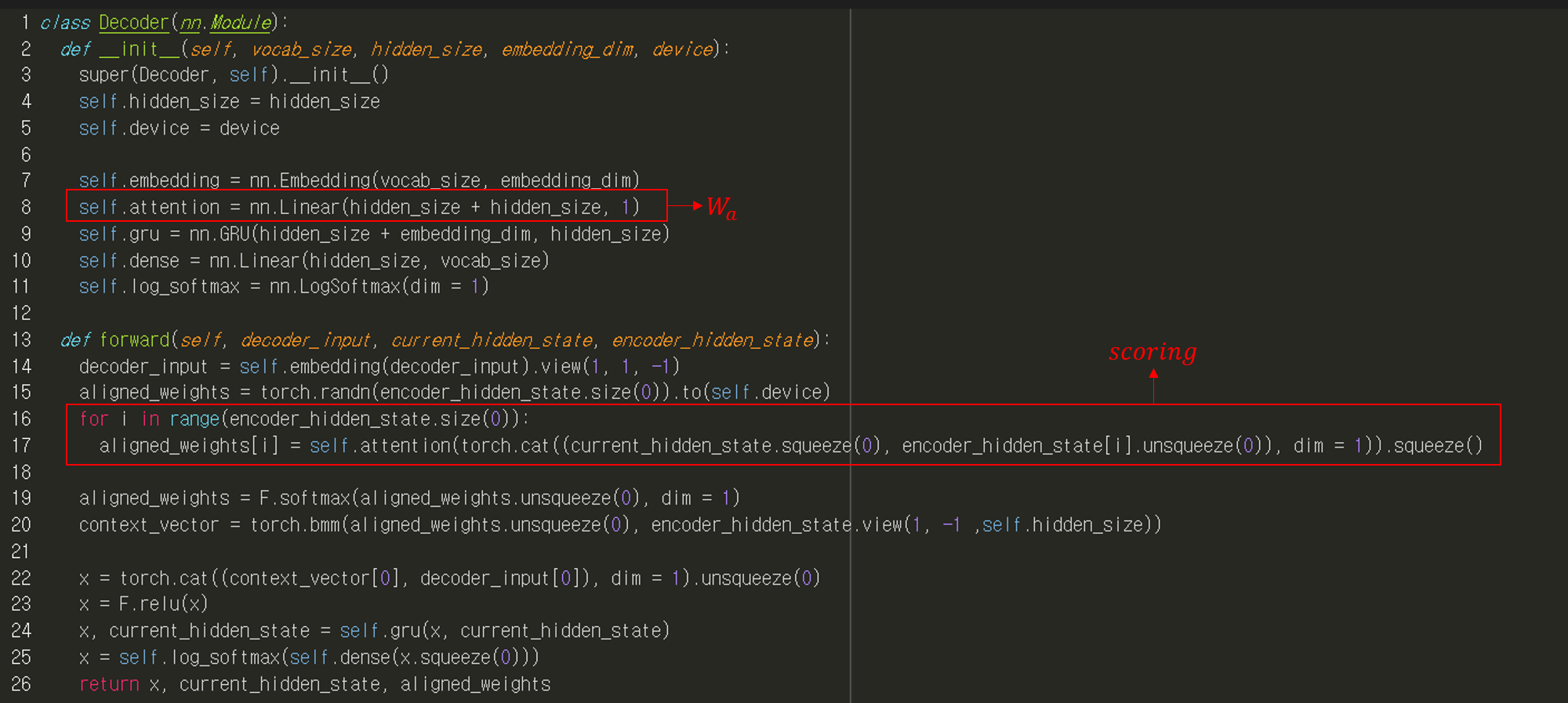
So far, we have implemented the scoring function as a simplified version of the concat function. Concat function, also known as additive function, was initially proposed by Bahdahanu et al. (2015). The concat function concatenates the source and target hidden states ($h_t, \bar{h_s}$), followed by a multiplication by the matrix $W_a$. Then, the multiplied result is passed onto a tangent hyperbolic activation ($tanh$) and then a dot product with another parameter $v_a^{T}$. However, we ommitted the tangent hyperbolic activation and parameter $v_a^{T}$ so far for simplicity. Therefore, what we have been implementing was, in mathematical formula:

\begin{equation} score(h_t, \bar{h_s}) = v_a^{T}tanh(W_a[h_t;\bar{h_s}]) \end{equation}

In Pytorch, it was implemented as below. Below is step-by-step procedure of the scoring operation.

• torch.cat() function concatenates source and target states
• self.attention layer multiplies W_a and the concatenated states
• for loop iterates over each step in the encoder
• F.softmax() function normalizes scored weights.

Concat (additive)

For the concat function, not the simplified one, we just need to add an activation and dot product with $v_a^{T}$. Therefore, in the init() function of the decoder class, we define another parameter vt for $v_a^{T}$. This parameter will be jointly trained with other parameters in the network.

self.attention = nn.Linear(hidden_size + hidden_size, hidden_size)
self.vt = nn.Parameter(torch.FloatTensor(1, hidden_size))

In the forward function, we just need to add few things. F.tanh() function will apply the tangent hyperbolic activation over matrix-multiplied outputs. Then, torch.dot() function will perform the dot product of the parameter and the intermediate output.

for i in range(encoder_hidden_state.size(0)):
    w = F.tanh(self.attention(torch.cat((current_hidden_state.squeeze(0), encoder_hidden_state[i].unsqueeze(0)), dim = 1)))
    aligned_weights[i] = torch.dot(self.vt.squeeze(), w.squeeze())

General

The general scoring function is simpler than the concat function. Instead of concatenating $h_t$ and $\bar{h_s}$ and multiplying with the matrix $W_a$, the general function multiplies $h_t$, $W_a$, and $\bar{h_s}$

\begin{equation} score(h_t, \bar{h_s}) = h_t^{T}W_a\bar{h_s} \end{equation}

Therefore, for the general function we only need the dense layer that performs matrix multiplication by $W_a$. However, note that self.attention layer here has the input size of hidden_size, instead of hidden_size * 2 as in the concat function. This difference in input dimension arises because the two hidden states are not concatenated in the general scoring function. Therefore, the input size of the general function is equal to the hidden size of \bar{h_s}.

self.attention = nn.Linear(hidden_size, hidden_size)

The computation of weights are also simpler. The source hidden states (encoder_hidden_state) are multiplied with $W_a$ by self.attention() and then dot-producted with the target hidden state (current_hidden_state).

aligned_weights[i] = torch.dot(current_hidden_state.squeeze(), self.attention(encoder_hidden_state[i].unsqueeze(0)).squeeze())

Dot

The dot scoring function is the most straightforward one. It is consisted of just a dot product of two hidden states ($h_t, \bar{h_s}$). No additional parameters to be defined and learned. We just need to multiply them with torch.dot() function to calculate the weights.

aligned_weights[i] = torch.dot(current_hidden_state.squeeze(), encoder_hidden_state[i].squeeze())  

Decoder - putting it altogether

It would be cumbersome to define a different decoder class everytime for a different scoring function. Therefore, we manage is with an additional parameter scoring that denotes the type of scoring function that is going to be used. Below is the decoder class that takes into account choosing different scoring functions.

class Decoder(nn.Module):
  def __init__(self, vocab_size, hidden_size, embedding_dim, scoring, device):
    super(Decoder, self).__init__()
    self.hidden_size = hidden_size
    self.device = device
    self.scoring = scoring

    self.embedding = nn.Embedding(vocab_size, embedding_dim)

    if scoring == "concat":
      self.attention = nn.Linear(hidden_size + hidden_size, hidden_size)
      self.vt = nn.Parameter(torch.FloatTensor(1, hidden_size))
    elif scoring == "general":
      self.attention = nn.Linear(hidden_size, hidden_size)
    self.gru = nn.GRU(hidden_size + embedding_dim, hidden_size)
    self.dense = nn.Linear(hidden_size, vocab_size)
    self.log_softmax = nn.LogSoftmax(dim = 1)
  
  def forward(self, decoder_input, current_hidden_state, encoder_hidden_state):
    decoder_input = self.embedding(decoder_input).view(1, 1, -1)
    aligned_weights = torch.randn(encoder_hidden_state.size(0)).to(self.device)

    if self.scoring == "concat":
      for i in range(encoder_hidden_state.size(0)):
        w = F.tanh(self.attention(torch.cat((current_hidden_state.squeeze(0), encoder_hidden_state[i].unsqueeze(0)), dim = 1)))
        aligned_weights[i] = torch.dot(self.vt.squeeze(), w.squeeze())
  
    elif self.scoring == "general":
      for i in range(encoder_hidden_state.size(0)):
        aligned_weights[i] = torch.dot(current_hidden_state.squeeze(), self.attention(encoder_hidden_state[i].unsqueeze(0)).squeeze())

    elif self.scoring == "dot":
      for i in range(encoder_hidden_state.size(0)):
        aligned_weights[i] = torch.dot(current_hidden_state.squeeze(), encoder_hidden_state[i].squeeze())    

    aligned_weights = F.softmax(aligned_weights.unsqueeze(0), dim = 1)
    context_vector = torch.bmm(aligned_weights.unsqueeze(0), encoder_hidden_state.view(1, -1 ,self.hidden_size))
    
    x = torch.cat((context_vector[0], decoder_input[0]), dim = 1).unsqueeze(0)
    x = F.relu(x)
    x, current_hidden_state = self.gru(x, current_hidden_state)
    x = self.log_softmax(self.dense(x.squeeze(0)))
    return x, current_hidden_state, aligned_weights

In this posting, we tried implementing various scoring function delineated in Luong et al. (2015). So far, we implemented just global attention mechanism. In the following postings, let’s have a look into how local attention can be implemented.

References

• Luong et al. (2015)