In the previous posting, we went through how users and items can be represented as vectors and their interaction records are expressed as a matrix. Then, we have seen how the distance (similarity) between users (or items) can be computed using vector representations. In this posting, let’s look deeper into how the distances can be calculated using diverse schemes.

User-item interaction matrix revisited

Let’s go back to the movie recommendation system with five users Tony, Willie, Wiggum, Nelson, and Krusty. They rated six movies, which are The Godfather, Inception, Leon, The Departed, Pulp Fiction, and Forrest Gump, on a 10-point scale.

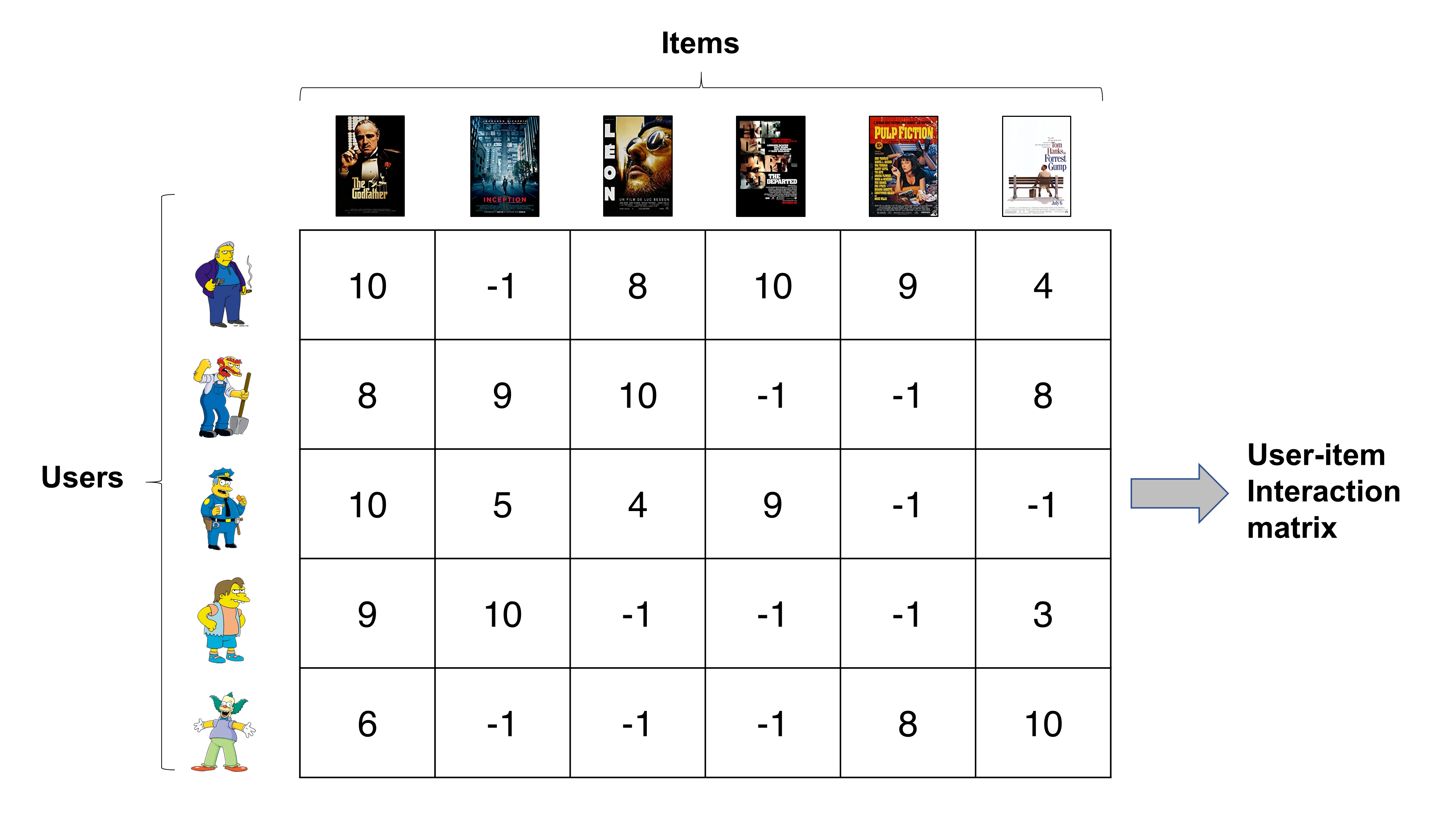
In the previous posting, we have discussed how to calculate the distance between two users using the Manhattan distance metric. Manhattan distance is basically the sum of the absolute values from element-wise subtraction. From the matrix above, we just need to retrieve elements in the corresponding rows and perform necessary operations on them, after excluding unobserved entries. For instance, the Manhattan distance between Tony and Krusty can be calculated as below.

\begin{equation} |v_{tony} - v_{krusty}| = |(4, -1, -1, -1, 1, 6)| = 11 \end{equation}

The distance between items can be calculated in a similar manner. We just need to use corresponding columns, instead of rows in this case. We can see that the movie The Godfather is more close to the movie Leon than the movie Forrest Gump.

\begin{equation} |v_{the \ godfather} - v_{forrest \ gump}| = |(6, 0, 6, -4)| = 16 \end{equation}

\begin{equation} |v_{the \ godfather} - v_{leon}| = |(2, -2, 6)| = 10 \end{equation}

Correlation-based similarity

Correlation-based similarity is another common-sensical way to measure the proximity between users or items. Remember that collaborative filtering is also known as “people-to-people” correlation method? We can calculate how two users (or items) correlate with each other using correlation coefficients. The most widely used correlation metric is the Pearson correlation coefficient. Pearson correlation similarity between two users u and v can be calculated as follows:

\begin{equation} corr(u, v) = \frac{\displaystyle\sum_{i \in I}(r_{ui} - \bar{r_u})(r_{vi} - \bar{r_v})}{\sqrt{\displaystyle\sum_{i \in I}(r_{ui} - \bar{r_u})^2 \displaystyle\sum_{i \in I}(r_{vi} - \bar{r_v})^2}} \end{equation}

, where $I$ is the items commonly rated by users u and v, $r_{ui}$ and $r_{vi}$ are ratings given to the item $i$ by u and v respectively. Finally, $\bar{r_u}$ and $\bar{r_v}$ are the average ratings given by u and v respectively.

Image source

The numerator of the metric measures how the ratings by the two users tend to vary in a similar fashion to each other. Hence, this part is also known as covariance. The denominator scales this measure, confining its values between -1 and 1.

Mean squared diffrence (MSD)

MSD is another popular similarity metric. It is the inverse of the mean squared difference of ratings between users u and v. Note that it is expressed as an inverse of the difference to indicate how similar two users (items) are. Furthermore, MSD is similar to the Pearson Correlation coefficient since it also tries to capture normalized covariant pattenrs between user ratings. Nonetheless, MSD does not take into account negative correlation since it can only take positive values.

\begin{equation} MSD(u, v) = \frac{|I|}{\sqrt{\displaystyle\sum_{i \in I}(r_{ui} - r_{vi})^2}} \end{equation}

Other similarity metrics

So far, we have seen three widely used similarity (distance) metrics. However, there are many other metrics such as cosine similarity, Jaccard similarity, and Spearman rank correlation. As in any other data mining problem, I should say there is no one-size-fits-all method to measure the level of similarity. Furthermore, you can define your own similarity function that suits the problem context! All metrics have their own pros and cons and you can be creative to complement limitations of existing approaches. In the following posting, let’s see how we can use calculated similarity metrics to recommend items to a user.

References

• Ricci, F., Rokach, L., & Shapira, B. (2011). Introduction to recommender systems handbook. In Recommender systems handbook (pp. 1-35). Springer, Boston, MA.
• Sarwar, B., Karypis, G., Konstan, J., & Riedl, J. (2001, April). Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th international conference on World Wide Web (pp. 285-295).