Attention in Neural Networks - 21. Transformer (5)
27 Apr 2020 | Attention mechanism Deep learning PytorchAttention Mechanism in Neural Networks - 21. Transformer (5)
In addition to improved performance and alignment between the input and output, attention mechanism provides possible explanations for how the model works. Despite the controversy over the “explainability” of attention mechanisms (e.g., Jain and Wallace, Wiegreffe and Pinter), examining attention weights is one of the few possible ways to understand the inner workings of complex deep neural network systems. However, nn.Transformer does not provide us with innate functionalities to extract and visualize weights. But the good news is that with just a few adjustments and tweaks using the original source code, we can make them fetch the weights and visualize them with matplotlib.
Data import & processing
As we did in the previous posting, let’s import the IMDB movie review sample dataset from the fastai library. But, let’s keep the maximum length of the sequence to 10 for fast and simple implementation.
from fastai.text import *
path = untar_data(URLs.IMDB_SAMPLE)
data = pd.read_csv(path/'texts.csv')
MAX_REVIEW_LEN = 10
reviews, labels = [], []
unique_tokens = set()
for i in tqdm(range(len(data))):
review = [x.lower() for x in re.findall(r"\w+", data.iloc[i]["text"])]
if len(review) >= MAX_REVIEW_LEN:
review = review[:MAX_REVIEW_LEN]
else:
for _ in range(MAX_REVIEW_LEN - len(review)):
review.append("<pad>")
reviews.append(review)
unique_tokens.update(review)
if data.iloc[i]["label"] == 'positive':
labels.append(1)
else:
labels.append(0)
unique_tokens = list(unique_tokens)
# print the size of the vocabulary
print(len(unique_tokens))
# encode each token into index
for i in tqdm(range(len(reviews))):
reviews[i] = [unique_tokens.index(x) for x in reviews[i]]
Example of processed (and raw) review text.
print(reviews[5])
print([unique_tokens[x] for x in reviews[5]])
Setting parameters
Setting parameters is fairly similar to the previous posting. But, since there is no target sequence to predict and we will not make use of the decoder, so parameter settings related to those are unnecessary. Instead, we need an additional hyperparameter of NUM_LABELS that indicates the number of classes in the target variable.
VOCAB_SIZE = len(unique_tokens)
NUM_EPOCHS = 100
HIDDEN_SIZE = 16
EMBEDDING_DIM = 30
BATCH_SIZE = 128
NUM_HEADS = 3
NUM_LAYERS = 3
NUM_LABELS = 2
DROPOUT = .5
LEARNING_RATE = 1e-3
DEVICE = torch.device('cuda')
Creating dataset & dataloader
We split the dataset to training and test data in 8-2 ratio, resulting in 800 training instances and 200 test instances.
class IMDBDataset(torch.utils.data.Dataset):
def __init__(self):
# import and initialize dataset
self.x = np.array(reviews, dtype = int)
self.y = np.array(labels, dtype = int)
def __getitem__(self, idx):
# get item by index
return self.x[idx], self.y[idx]
def __len__(self):
# returns length of data
return len(self.x)
np.random.seed(777) # for reproducibility
dataset = IMDBDataset()
NUM_INSTANCES = len(dataset)
TEST_RATIO = 0.2
TEST_SIZE = int(NUM_INSTANCES * 0.2)
indices = list(range(NUM_INSTANCES))
test_idx = np.random.choice(indices, size = TEST_SIZE, replace = False)
train_idx = list(set(indices) - set(test_idx))
train_sampler, test_sampler = SubsetRandomSampler(train_idx), SubsetRandomSampler(test_idx)
train_loader = torch.utils.data.DataLoader(dataset, batch_size = BATCH_SIZE, sampler = train_sampler)
test_loader = torch.utils.data.DataLoader(dataset, batch_size = BATCH_SIZE, sampler = test_sampler)
Multihead attention
As explained earlier, nn.Transformer makes use of nn.MultiheadAttention module which performs the multihead attention operation given queries, keys, and values. If we closely examine the source code, it has two outputs, i.e., attn_output and attn_output_weights.
So far, we only utilized attn_output that is fed into the final dense layer for classification. We can explicitly observe this from the first line of the forward function TransformerEncoderLayer. (self.self_attn is defined as MultiheadAttention(d_model, nhead, dropout=dropout) in the initialization process).
def forward(self, src, src_mask=None, src_key_padding_mask=None):
src2 = self.self_attn(src, src, src, attn_mask=src_mask, key_padding_mask= src_key_padding_mask)[0]
So, our strategy will be utilizing attn_output_weights that shows the alignment between the target and source. To do so, we will make use of both inputs from self.self.attn().
Transformer encoder layer
First and foremost, we need to make adjustment to TransformerEncoderLayer. After defining the _get_activation_fn function, add nn. to each module, e.g., MultiheadAttention(d_model, nhead, dropout=dropout) to nn.MultiheadAttention(d_model, nhead, dropout=dropout). And most important, record the alignment weights from self.self_attn, i.e., the multihead attention, and return it with the attention output(src2).
def _get_activation_fn(activation):
if activation == "relu":
return F.relu
elif activation == "gelu":
return F.gelu
raise RuntimeError("activation should be relu/gelu, not {}".format(activation))
class TransformerEncoderLayer(Module):
def __init__(self, d_model, nhead, dim_feedforward=2048, dropout=0.1, activation="relu"):
super(TransformerEncoderLayer, self).__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
# Implementation of Feedforward model
self.linear1 = nn.Linear(d_model, dim_feedforward)
self.dropout = nn.Dropout(dropout)
self.linear2 = nn.Linear(dim_feedforward, d_model)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout1 = nn.Dropout(dropout)
self.dropout2 = nn.Dropout(dropout)
self.activation = _get_activation_fn(activation)
def __setstate__(self, state):
if 'activation' not in state:
state['activation'] = F.relu
super(TransformerEncoderLayer, self).__setstate__(state)
def forward(self, src, src_mask=None, src_key_padding_mask=None):
# type: (Tensor, Optional[Tensor], Optional[Tensor]) -> Tensor
src2, weights = self.self_attn(src, src, src, attn_mask=src_mask,
key_padding_mask=src_key_padding_mask)
src = src + self.dropout1(src2)
src = self.norm1(src)
src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
src = src + self.dropout2(src2)
src = self.norm2(src)
return src, weights
Transformer encoder
Now we can make adjustments to the transformer encoder. First, define _get_clones function that copies encoder layers. Do not forget to import copy and and nn. to ModuleList. And, similar to what we did before, we need to record the calculated alignment weights. Let’s explicitly make a list weights to save the weight from each layer. Again, this layer has to be returned with the final attention output.
import copy
def _get_clones(module, N):
return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
class TransformerEncoder(Module):
__constants__ = ['norm']
def __init__(self, encoder_layer, num_layers, norm=None):
super(TransformerEncoder, self).__init__()
self.layers = _get_clones(encoder_layer, num_layers)
self.num_layers = num_layers
self.norm = norm
def forward(self, src, mask=None, src_key_padding_mask=None):
# type: (Tensor, Optional[Tensor], Optional[Tensor]) -> Tensor
output = src
weights = []
for mod in self.layers:
output, weight = mod(output, src_mask=mask, src_key_padding_mask=src_key_padding_mask)
weights.append(weight)
if self.norm is not None:
output = self.norm(output)
return output, weights
Transformer
Finally, we can define the entire Transformer architecture with the building blocks. The process of fetching and returning both weights and outputs is similar to what we did with RNN Encoder-Decoders.
class TransformerNet(nn.Module):
def __init__(self, num_vocab, embedding_dim, hidden_size, nheads, n_layers, max_len, num_labels, dropout):
super(TransformerNet, self).__init__()
# embedding layer
self.embedding = nn.Embedding(num_vocab, embedding_dim)
# positional encoding layer
self.pe = PositionalEncoding(embedding_dim, max_len = max_len)
# encoder layers
enc_layer = TransformerEncoderLayer(embedding_dim, nheads, hidden_size, dropout)
self.encoder = TransformerEncoder(enc_layer, num_layers = n_layers)
# final dense layer
self.dense = nn.Linear(embedding_dim*max_len, num_labels)
self.log_softmax = nn.LogSoftmax()
def forward(self, x):
x = self.embedding(x).permute(1, 0, 2)
x = self.pe(x)
x, w = self.encoder(x)
x = x.reshape(x.shape[1], -1)
x = self.dense(x)
return x, w
model = TransformerNet(VOCAB_SIZE, EMBEDDING_DIM, HIDDEN_SIZE, NUM_HEADS, NUM_LAYERS, MAX_REVIEW_LEN, NUM_LABELS, DROPOUT).to(DEVICE)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr = LEARNING_RATE)
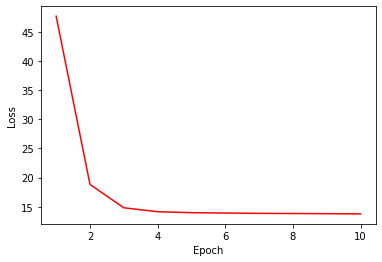
Training
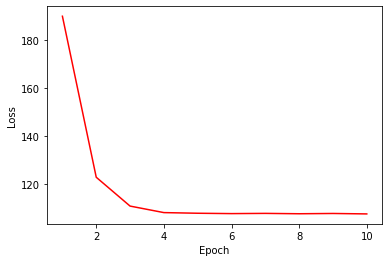
Training is also straightforward, just be aware of recording the weights (w) from the model.
%%time
loss_trace = []
for epoch in tqdm(range(NUM_EPOCHS)):
current_loss = 0
for i, (x, y) in enumerate(train_loader):
x, y = x.to(DEVICE), y.to(DEVICE)
outputs, w = model(x)
loss = criterion(outputs, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
current_loss += loss.item()
loss_trace.append(current_loss)
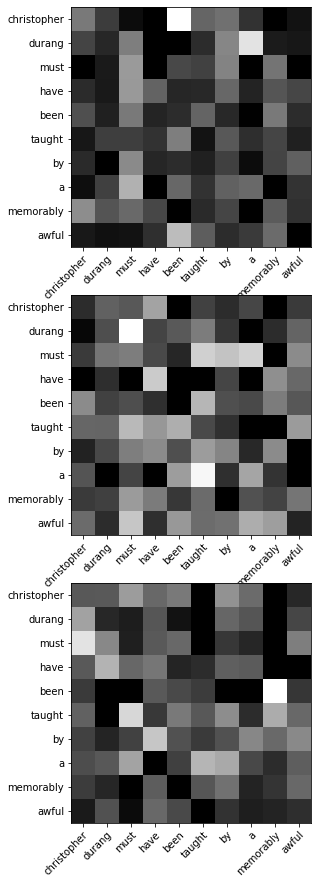
Visualization
Let’s try visualizing the alignment weights for the last training instance. w list has three tensors as elements, each as outputs from each encoder layer. Each tensor has the shape of (N, S, S), or (batch size, source sequence length, source sequence length).
print(len(w))
print(w[0].shape)
input_sentence = x[-1].detach().cpu().numpy()
input_sentence = [unique_tokens[x] for x in input_sentence]
fig, axes = plt.subplots(nrows = 3, ncols = 1, figsize = (5, 15), facecolor = "w")
for i in range(len(w)):
axes[i].imshow(w[i][-1].detach().cpu().numpy(), cmap = "gray")
axes[i].set_yticks(np.arange(len(input_sentence)))
axes[i].set_yticklabels(input_sentence)
axes[i].set_xticks(np.arange(len(input_sentence)))
axes[i].set_xticklabels(input_sentence)
plt.setp(axes[i].get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
plt.show()
[Image source: Vaswani et al. (2017)]
[Image source: Vaswani et al. (2017)]
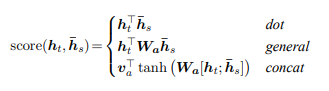
[Image source: Cheng et al. (2016)]
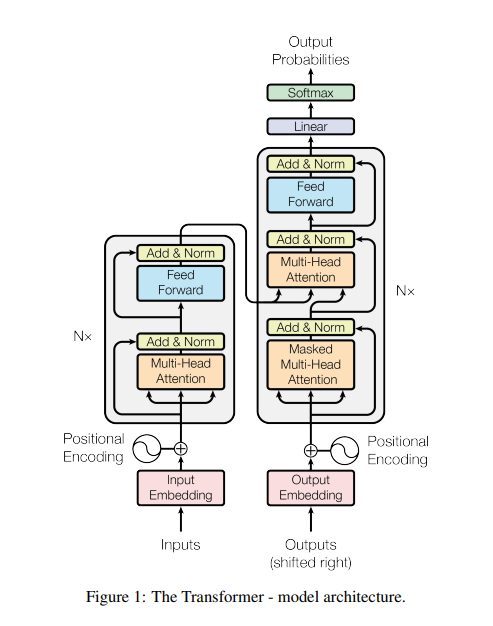[Image source: Vaswani et al. (2017)]