Attention Mechanism in Neural Networks - 7. Sequence-to-Sequence (Seq2Seq) (6)
In the previous posting, we tried implementing another variant of the Seq2Seq model presented by Sutskever et al. (2014). Two key improvements in the variant, i.e., deep LSTM layers and reversing the order of input sequences, are claimed to significantly enhance the performances, especially in the existence of big data.
However, large data implies large computing and it often takes a huge amount of resources to train deep learning models, especially those having complicated structures such as Seq2Seq. There are many methods to expedite the learning process of large-scale deep learning models. One of the basic approaches is applying the mini-batch Stochastic Gradient Descent (SGD) to achieve faster iterations.
So far, we have trained and updated model weights after looking at one instance at a time. On another extreme, we can try updating the weights after looking the whole dataset. Naturally, this can be much faster in iterating, though with a lower convergence rate. In practice, we commonly choose to strike a balance between the two. In other words, we partition the training dataset in small chunks, i.e., “batches,” and update the weights after examining each batch.
Therefore, in this posting, we look into implemeting a mini-batch SGD version of the Seq2Seq model. This would be basically the same model as those in previous postings, but guarantees faster training. I acknowledge that I had a great help in converting the code from PyTorch Seq2Seq tutorials.
Import packages & download dataset
For mini-batch implementation, we take advantage of torch.utils.data to generate custom datasets and dataloaders. For more information, please refer to Generating Data in PyTorch
import re
import torch
import numpy as np
import torch.nn as nn
from matplotlib import pyplot as plt
from torch.utils.data.sampler import SubsetRandomSampler
from tqdm import tqdm
!wget https://www.manythings.org/anki/deu-eng.zip
!unzip deu-eng.zip
with open("deu.txt") as f:
sentences = f.readlines()
# number of sentences
len(sentences)
Data processing
One trick to easier mini-batch implementation of Seq2Seq, or any sequence models, is to set the length of sequences identical. By doing so, we can make mini-batch computation much easier, which is often three- or four-dimensional tensor multiplications. Here, I have set the maximum length of source and target sentences (MAX_SENT_LEN) to 10. Then, sentences that are shorter than 10 are padded with <pad> tokens and those longer than 10 are trimmed to fit in. However, note that doing so can lead to a loss of information due to trimming. If you want to evade such loss, you can set MAX_SENT_LEN to actual maximum length of source and target sentences. On the othe hand, this can be set arbitrarily. If you want faster computation despite the loss of information, you can set the value shorter than I did.
NUM_INSTANCES = 50000
MAX_SENT_LEN = 10
eng_sentences, deu_sentences = [], []
eng_words, deu_words = set(), set()
for i in tqdm(range(NUM_INSTANCES)):
rand_idx = np.random.randint(len(sentences))
# find only letters in sentences
eng_sent, deu_sent = ["<sos>"], ["<sos>"]
eng_sent += re.findall(r"\w+", sentences[rand_idx].split("\t")[0])
deu_sent += re.findall(r"\w+", sentences[rand_idx].split("\t")[1])
# change to lowercase
eng_sent = [x.lower() for x in eng_sent]
deu_sent = [x.lower() for x in deu_sent]
eng_sent.append("<eos>")
deu_sent.append("<eos>")
if len(eng_sent) >= MAX_SENT_LEN:
eng_sent = eng_sent[:MAX_SENT_LEN]
else:
for _ in range(MAX_SENT_LEN - len(eng_sent)):
eng_sent.append("<pad>")
if len(deu_sent) >= MAX_SENT_LEN:
deu_sent = deu_sent[:MAX_SENT_LEN]
else:
for _ in range(MAX_SENT_LEN - len(deu_sent)):
deu_sent.append("<pad>")
# add parsed sentences
eng_sentences.append(eng_sent)
deu_sentences.append(deu_sent)
# update unique words
eng_words.update(eng_sent)
deu_words.update(deu_sent)
The rest is identical. It is up to your choice to reverse the order of the source inputs or not. For more information refer to the previous posting.
eng_words, deu_words = list(eng_words), list(deu_words)
# encode each token into index
for i in tqdm(range(len(eng_sentences))):
eng_sentences[i] = [eng_words.index(x) for x in eng_sentences[i]]
deu_sentences[i] = [deu_words.index(x) for x in deu_sentences[i]]
idx = 10
print(eng_sentences[idx])
print([eng_words[x] for x in eng_sentences[idx]])
print(deu_sentences[idx])
print([deu_words[x] for x in deu_sentences[idx]])
You can see that short sentences are padded with <pad> as below.
[5260, 7633, 4875, 2214, 6811, 2581, 2581, 2581, 2581, 2581]
['<sos>', 'you', 'amuse', 'me', '<eos>', '<pad>', '<pad>', '<pad>', '<pad>', '<pad>']
[9284, 13515, 2514, 9574, 11982, 4432, 4432, 4432, 4432, 4432]
['<sos>', 'ihr', 'amüsiert', 'mich', '<eos>', '<pad>', '<pad>', '<pad>', '<pad>', '<pad>']
Setting parameters
One more parameter that is added is BATCH_SIZE. It is often set to values that are multiples of 16, e.g., 32, 64, 128, 256, 512, etc. However, this is also up to you. Just do not let it exceed total number of instances and consider the memory constraints of your GPU (or CPU)!
ENG_VOCAB_SIZE = len(eng_words)
DEU_VOCAB_SIZE = len(deu_words)
NUM_EPOCHS = 10
HIDDEN_SIZE = 128
EMBEDDING_DIM = 30
BATCH_SIZE = 128
LEARNING_RATE = 1e-2
DEVICE = torch.device('cuda')
Dataset and Dataloader
We need to define the dataset and dataloader for efficient implementation of mini-batch SGD. In this posting, we randomly partition the dataset in 7-3 ratio and generate train and test dataloaders. For more information on this part, please refer to Generating Data in PyTorch
class MTDataset(torch.utils.data.Dataset):
def __init__(self):
# import and initialize dataset
self.source = np.array(eng_sentences, dtype = int)
self.target = np.array(deu_sentences, dtype = int)
def __getitem__(self, idx):
# get item by index
return self.source[idx], self.target[idx]
def __len__(self):
# returns length of data
return len(self.source)
np.random.seed(777) # for reproducibility
dataset = MTDataset()
NUM_INSTANCES = len(dataset)
TEST_RATIO = 0.3
TEST_SIZE = int(NUM_INSTANCES * 0.3)
indices = list(range(NUM_INSTANCES))
test_idx = np.random.choice(indices, size = TEST_SIZE, replace = False)
train_idx = list(set(indices) - set(test_idx))
train_sampler, test_sampler = SubsetRandomSampler(train_idx), SubsetRandomSampler(test_idx)
train_loader = torch.utils.data.DataLoader(dataset, batch_size = BATCH_SIZE, sampler = train_sampler)
test_loader = torch.utils.data.DataLoader(dataset, batch_size = BATCH_SIZE, sampler = test_sampler)
Encoder
The encoder is similary defined as previous postings. As we will be only needing the hidden state of the last GRU cell in the encoder, we reserve only the last h0 here. Also, note that the hidden state has size of (1, BATCH_SIZE, HIDDEN_SIZE) to incorporate batch learning.
class Encoder(nn.Module):
def __init__(self, vocab_size, hidden_size, embedding_dim, device):
super(Encoder, self).__init__()
self.hidden_size = hidden_size
self.vocab_size = vocab_size
self.device = device
self.embedding_dim = embedding_dim
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.gru = nn.GRU(embedding_dim, hidden_size)
def forward(self, x, h0):
# x = (BATCH_SIZE, MAX_SENT_LEN) = (128, 10)
x = self.embedding(x)
x = x.permute(1, 0, 2)
# x = (MAX_SENT_LEN, BATCH_SIZE, EMBEDDING_DIM) = (10, 128, 30)
out, h0 = self.gru(x, h0)
print(out.shape)
# out = (MAX_SENT_LEN, BATCH_SIZE, HIDDEN_SIZE) = (128, 10, 16)
# h0 = (1, BATCH_SIZE, HIDDEN_SIZE) = (1, 128, 16)
return out, h0
Decoder
The decoder is similarly trained but with a subtle difference of learning each step at a time. By doing so, we can save the output (x) and hidden state (h0) at every step.
class Decoder(nn.Module):
def __init__(self, vocab_size, hidden_size, embedding_dim):
super(Decoder, self).__init__()
self.hidden_size = hidden_size
self.vocab_size = vocab_size
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.gru = nn.GRU(embedding_dim, hidden_size)
self.dense = nn.Linear(hidden_size, vocab_size)
self.softmax = nn.LogSoftmax(dim = 1)
def forward(self, x, h0):
# x = (BATCH_SIZE) = (128)
x = self.embedding(x).unsqueeze(0)
# x = (1, BATCH_SIZE, EMBEDDING_DIM) = (1, 128, 30)
x, h0 = self.gru(x, h0)
x = self.dense(x.squeeze(0))
x = self.softmax(x)
return x, h0
Seq2Seq model
Here, we define the Seq2Seq model in a separate Python class. The first input to the Seq2Seq model is the token at the first timestep, i.e., “". We can designate this by slicing the ```target``` variable.
The resulting dec_input variable will have the shape of BATCH_SIZE. Then in each timestep, the decoder calculates the output from the current input (dec_input) and previous hidden state (h0). We also implement teacher forcing, in which we set the input to the next state as the actual target, not the predicted target. The probability of setting teacher forcing can be manipulated with the parameter tf_ratio. The default probability is 0.5.
class Seq2Seq(nn.Module):
def __init__(self, encoder, decoder, device):
super(Seq2Seq, self).__init__()
self.encoder = encoder
self.decoder = decoder
self.device = device
def forward(self, source, target, tf_ratio = .5):
# target = (BATCH_SIZE, MAX_SENT_LEN) = (128, 10)
# source = (BATCH_SIZE, MAX_SENT_LEN) = (128, 10)
dec_outputs = torch.zeros(target.size(0), target.size(1), self.decoder.vocab_size).to(self.device)
h0 = torch.zeros(1, source.size(0), self.encoder.hidden_size).to(self.device)
_, h0 = self.encoder(source, h0)
# dec_input = (BATCH_SIZE) = (128)
dec_input = target[:, 0]
for k in range(target.size(1)):
# out = (BATCH_SIZE, VOCAB_SIZE) = (128, XXX)
# h0 = (1, BATCH_SIZE, HIDDEN_SIZE) = (1, 128, 16)
out, h0 = self.decoder(dec_input, h0)
dec_outputs[:, k, :] = out
dec_input = target[:, k]
if np.random.choice([True, False], p = [tf_ratio, 1-tf_ratio]):
dec_input = target[:, k]
else:
dec_input = out.argmax(1).detach()
return dec_outputs
Defining the model
As we defined the Seq2Seq model, we only need to generate the optimizer for the whole model. No need to create separate optimizers for both encoder and decoder.
encoder = Encoder(ENG_VOCAB_SIZE, HIDDEN_SIZE, EMBEDDING_DIM, DEVICE).to(DEVICE)
decoder = Decoder(DEU_VOCAB_SIZE, HIDDEN_SIZE, EMBEDDING_DIM).to(DEVICE)
seq2seq = Seq2Seq(encoder, decoder, DEVICE).to(DEVICE)
criterion = nn.NLLLoss()
optimizer = torch.optim.Adam(seq2seq.parameters(), lr = LEARNING_RATE)
Training and evaluation
Training is much simpler when done this way. The seq2seq model does all computation for us. We just need to be mindful of calculating the loss. NLLLoss in Pytorch does not enable three-dimensional computation, so we have slightly resize the output and y.
%%time
loss_trace = []
for epoch in tqdm(range(NUM_EPOCHS)):
current_loss = 0
for i, (x, y) in enumerate(train_loader):
x, y = x.to(DEVICE), y.to(DEVICE)
outputs = seq2seq(x, y)
loss = criterion(outputs.resize(outputs.size(0) * outputs.size(1), outputs.size(-1)), y.resize(y.size(0) * y.size(1)))
optimizer.zero_grad()
loss.backward()
optimizer.step()
current_loss += loss.item()
loss_trace.append(current_loss)
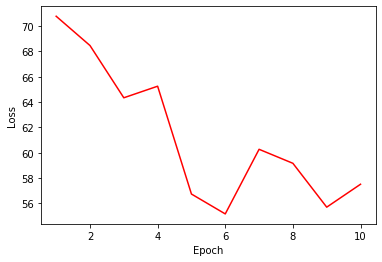
# loss curve
plt.plot(range(1, NUM_EPOCHS+1), loss_trace, 'r-')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()
For evaluation, we calculate all predictions and save them in a list (predictions). Then we can access them with indices as we did with inputs.
predictions = []
for i, (x,y) in enumerate(test_loader):
with torch.no_grad():
x, y = x.to(DEVICE), y.to(DEVICE)
outputs = seq2seq(x, y)
for output in outputs:
_, indices = output.max(-1)
predictions.append(indices.detach().cpu().numpy())
idx = 10 # index of the sentence that you want to demonstrate
# print out the source sentence and predicted target sentence
print([eng_words[i] for i in eng_sentences[idx]])
print([deu_words[i] for i in predictions[idx]])
['<sos>', 'you', 'amuse', 'me', '<eos>', '<pad>', '<pad>', '<pad>', '<pad>', '<pad>']
['<sos>', 'ich', 'ist', 'nicht', '<eos>', '<eos>', '<eos>', '<pad>', '<pad>', '<pad>']
In this posting, we looked into implementing mini-batch SGD for Seq2Seq. This will enable much faster computation in most cases. So far through six postings, we have dealt with Seq2Seq model in depth. From next posting, let us gently introduce ourselves to the Alignment model, which is the initial attempt to implement attention models. Thank you for reading.
References