Attention in Neural Networks - 16. Hierarchical Attention (2)
26 Mar 2020 | Attention mechanism Deep learning PytorchAttention Mechanism in Neural Networks - 16. Hierarchical Attention (2)
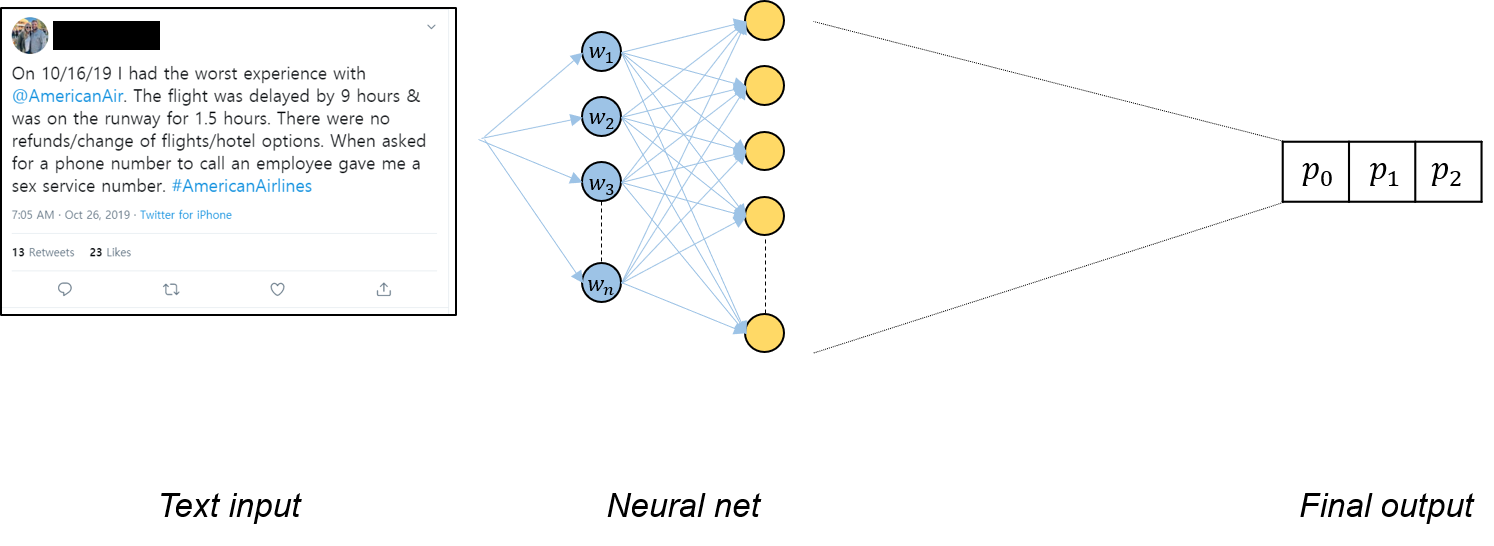
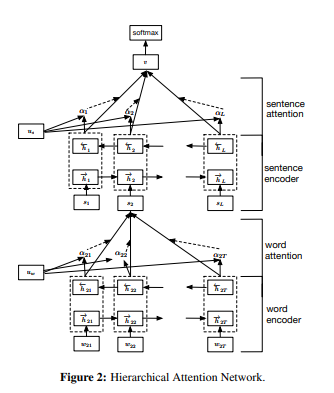
In the previous posting, we had a first look into the hierarchical attention network (HAN) for document classification. HAN is a two-level neural network architecture that fully takes advantage of hierarchical features in text data. Also, it considers interaction between words and sentences by adapting the attention mechanism. In this posting, let’s try implementing HAN with Pytorch.
Data import
Since we are implementing a document classification model rather than one for machine translation, we need a different dataset. The dataset that I have chosen is the Twitter self-driving sentiment dataset provided by Crowdflower. It contains tweets regarding self-driving cars, tagged as very positive, slightly positive, neutral, slightly negative, or very negative. The dataset can be easily downloaded via a hyperlink, using Pandas read.csv() function.
data = pd.read_csv("https://d1p17r2m4rzlbo.cloudfront.net/wp-content/uploads/2016/03/Twitter-sentiment-self-drive-DFE.csv", encoding = 'latin-1')
data.head()
The imported data is in a dataframe format having 11 columns. Columns of interest here are sentiment and text.
_unit_id _golden _unit_state _trusted_judgments _last_judgment_at sentiment sentiment:confidence our_id sentiment_gold sentiment_gold_reason text
0 724227031 True golden 236 NaN 5 0.7579 10001 5\n4 Author is excited about the development of the... Two places I'd invest all my money if I could:...
1 724227032 True golden 231 NaN 5 0.8775 10002 5\n4 Author is excited that driverless cars will be... Awesome! Google driverless cars will help the ...
2 724227033 True golden 233 NaN 2 0.6805 10003 2\n1 The author is skeptical of the safety and reli... If Google maps can't keep up with road constru...
3 724227034 True golden 240 NaN 2 0.8820 10004 2\n1 The author is skeptical of the project's value. Autonomous cars seem way overhyped given the t...
4 724227035 True golden 240 NaN 3 1.0000 10005 3 Author is making an observation without expres... Just saw Google self-driving car on I-34. It w...
Preprocessing
Data preprocessing is done similarly to previous postings, but here we need to record scores for each tweet. The scores are recorded in the sent_scores list.
NUM_INSTANCES = 3000
MAX_SENT_LEN = 10
tweets, sent_scores = [], []
unique_tokens = set()
for i in tqdm(range(NUM_INSTANCES)):
rand_idx = np.random.randint(len(data))
# find only letters in sentences
tweet = []
sentences = data["text"].iloc[rand_idx].split(".")
for sent in sentences:
if len(sent) != 0:
sent = [x.lower() for x in re.findall(r"\w+", sent)]
if len(sent) >= MAX_SENT_LEN:
sent = sent[:MAX_SENT_LEN]
else:
for _ in range(MAX_SENT_LEN - len(sent)):
sent.append("<pad>")
tweet.append(sent)
unique_tokens.update(sent)
tweets.append(tweet)
if data["sentiment"].iloc[rand_idx] == 'not_relevant':
sent_scores.append(0)
else:
sent_scores.append(int(data["sentiment"].iloc[rand_idx]))
We have 6,266 unique tokens in the corpus after preprocessing.
unique_tokens = list(unique_tokens)
# print the size of the vocabulary
print(len(unique_tokens))
6266
The final step is to numericalize each token, just like we did before.
# encode each token into index
for i in tqdm(range(len(tweets))):
for j in range(len(tweets[i])):
tweets[i][j] = [unique_tokens.index(x) for x in tweets[i][j]]
Setting parameters
When setting hyperparameters, there are two major differences. First, we have only one set of text data, i.e., tweets, so we only need vocabulary size for that (VOCAB_SIZE). Then, we need to define NUM_CLASSES variable to indicate the number of target classes that we want to predict.
VOCAB_SIZE = len(unique_tokens)
NUM_CLASSES = len(set(sent_scores))
LEARNING_RATE = 1e-3
NUM_EPOCHS = 10
HIDDEN_SIZE = 16
EMBEDDING_DIM = 30
DEVICE = torch.device('cuda')
Encoders
Instead of generating an encoder and a decoder, we need to create two encoders for HAN - i.e., a word
encoder and sentence encoder. The two encoders are very similar to each other, except the additional embedding layer (self.embedding) in the word encoder to index words.
class wordEncoder(nn.Module):
def __init__(self, vocab_size, hidden_size, embedding_dim):
super(wordEncoder, self).__init__()
self.hidden_size = hidden_size
self.vocab_size = vocab_size
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.gru = nn.GRU(embedding_dim, hidden_size, bidirectional = True)
def forward(self, word, h0):
word = self.embedding(word).unsqueeze(0).unsqueeze(1)
out, h0 = self.gru(word, h0)
return out, h0
class sentEncoder(nn.Module):
def __init__(self, hidden_size):
super(sentEncoder, self).__init__()
self.hidden_size = hidden_size
self.gru = nn.GRU(hidden_size, hidden_size, bidirectional = True)
def forward(self, sentence, h0):
sentence = sentence.unsqueeze(0).unsqueeze(1)
out, h0 = self.gru(sentence)
return out, h0
Hierarchical attention network
Now we can define the HAN class to generate the whole network architecture. In the forward() function, just note that there are two for loops to iterate on sentences and words to consider the hierarchy in data. The first for loop having i as the index iterates on sentences while the second one having j iterates on words. The output from the sentence encoder (sentenc_out) is passed onto the final dense layer, calculating the (sentence-level) attention weights and class probabilities.
class HAN(nn.Module):
def __init__(self, wordEncoder, sentEncoder, num_classes, device):
super(HAN, self).__init__()
self.wordEncoder = wordEncoder
self.sentEncoder = sentEncoder
self.device = device
self.softmax = nn.Softmax(dim=1)
# word-level attention
self.word_attention = nn.Linear(self.wordEncoder.hidden_size*2, self.wordEncoder.hidden_size*2)
self.u_w = nn.Linear(self.wordEncoder.hidden_size*2, 1, bias = False)
# sentence-level attention
self.sent_attention = nn.Linear(self.sentEncoder.hidden_size * 2, self.sentEncoder.hidden_size*2)
self.u_s = nn.Linear(self.sentEncoder.hidden_size*2, 1, bias = False)
# final layer
self.dense_out = nn.Linear(self.sentEncoder.hidden_size*2, num_classes)
self.log_softmax = nn.LogSoftmax()
def forward(self, document):
word_attention_weights = []
sentenc_out = torch.zeros((document.size(0), 2, self.sentEncoder.hidden_size)).to(self.device)
# iterate on sentences
h0_sent = torch.zeros(2, 1, self.sentEncoder.hidden_size, dtype = float).to(self.device)
for i in range(document.size(0)):
sent = document[i]
wordenc_out = torch.zeros((sent.size(0), 2, self.wordEncoder.hidden_size)).to(self.device)
h0_word = torch.zeros(2, 1, self.wordEncoder.hidden_size, dtype = float).to(self.device)
# iterate on words
for j in range(sent.size(0)):
_, h0_word = self.wordEncoder(sent[j], h0_word)
wordenc_out[j] = h0_word.squeeze()
wordenc_out = wordenc_out.view(wordenc_out.size(0), -1)
u_word = torch.tanh(self.word_attention(wordenc_out))
word_weights = self.softmax(self.u_w(u_word))
word_attention_weights.append(word_weights)
sent_summ_vector = (u_word * word_weights).sum(axis=0)
_, h0_sent = self.sentEncoder(sent_summ_vector, h0_sent)
sentenc_out[i] = h0_sent.squeeze()
sentenc_out = sentenc_out.view(sentenc_out.size(0), -1)
u_sent = torch.tanh(self.sent_attention(sentenc_out))
sent_weights = self.softmax(self.u_s(u_sent))
doc_summ_vector = (u_sent * sent_weights).sum(axis=0)
out = self.dense_out(doc_summ_vector)
return word_attention_weights, sent_weights, self.log_softmax(out)
Training
Now, let’s try training the HAN model. Just note that there are two attention weights calculated from the model, word_weights and sent_weights. Such weights can be used to examine instance-level interactions between words and sentences of interest.
word_encoder = wordEncoder(VOCAB_SIZE, HIDDEN_SIZE, EMBEDDING_DIM).to(DEVICE)
sent_encoder = sentEncoder(HIDDEN_SIZE * 2).to(DEVICE)
model = HAN(word_encoder, sent_encoder, NUM_CLASSES, DEVICE).to(DEVICE)
optimizer = torch.optim.Adam(model.parameters(), lr = LEARNING_RATE)
criterion = nn.NLLLoss()
%%time
loss = []
weights = []
for i in tqdm(range(NUM_EPOCHS)):
current_loss = 0
for j in range(len(tweets)):
tweet, score = torch.tensor(tweets[j], dtype = torch.long).to(DEVICE), torch.tensor(sent_scores[j]).to(DEVICE)
word_weights, sent_weights, output = model(tweet)
optimizer.zero_grad()
current_loss += criterion(output.unsqueeze(0), score.unsqueeze(0))
current_loss.backward(retain_graph=True)
optimizer.step()
loss.append(current_loss.item()/(j+1))